La moyenne et son rôle dans l’évaluation immobilière
Évaluation immobilière au Canada
Rechercher dans la bibliothèque en ligne
Par George Canning, AACI, P. App., Canning Consultants Inc., London, ON
Il ne fait aucun doute que la moyenne de toute série de nombres est importante. Dans son article, intitulé The Strange Power of the Idea of Average [L’étrange pouvoir de l’idée d’une moyenne], publié dans le Financial Times du 2 août 2019, Tim Harford déclare : « C’est l’opération statistique la plus radicale jamais imaginée… La moyenne possède un pouvoir étrange sur notre façon de penser, et pas toujours un pouvoir bénin. »
Nul ne sait qui a inventé la moyenne arithmétique. Elle a beaucoup servi à mesurer les observations et à éliminer les erreurs dans les données de quelqu’un. Dès les années 1800, simplement utiliser une moyenne était considéré comme un piège, puisque toutes les autres observations dans une série particulière de données n’étaient pas nécessairement des erreurs ou sans importance. En d’autres mots, il existe une valeur à comprendre la moyenne d’une série de nombres, mais aussi le rapport de la moyenne avec d’autres points de données. Alors qu’il y a d’autres types de moyenne comme géométrique, pondéré et harmonique, nous allons utiliser la moyenne la plus familière à la plupart des évaluateurs.
La principale question pour les évaluateurs, c’est pourquoi ils ne peuvent pas prendre la moyenne d’une série de données de vente et conclure que c’est la valeur marchande de la propriété évaluée. Il est certain que plusieurs évaluateurs ont fait cela, seulement pour se rendre compte que la démarche est remplie d’erreurs.
À titre d’illustration, j’ai évalué ma maison à partir des ventes effectuées après le 1er janvier 2017, dans des culs-de-sac similaires de mon voisinage. Le graphique 1 est le nuage statistique des données de vente selon la superficie en pieds carrés des maisons à vendre.
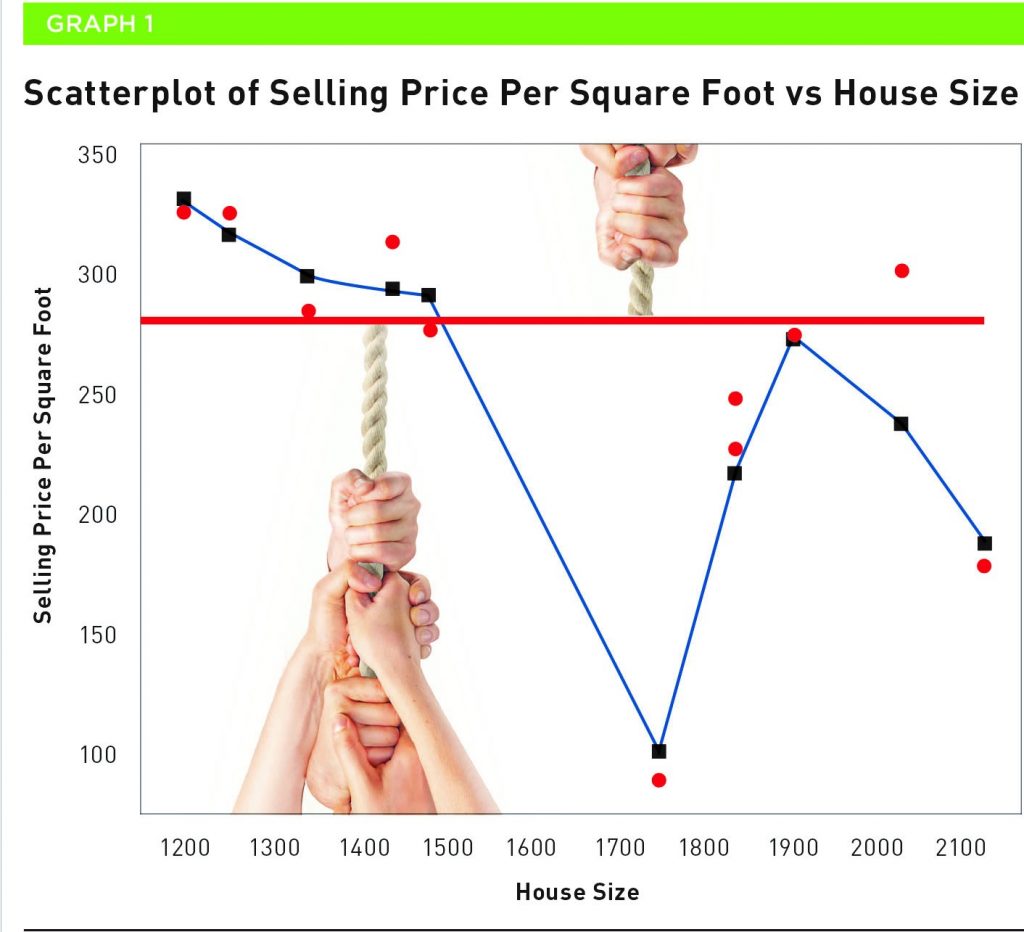
La ligne rouge est la moyenne des données de vente, à 258,09 $ le pied carré de maison. La ligne bleue est un lisseur Lowess. Comme ce nom l’indique, il est utilisé pour lisser, ou aplanir, la forme des données. Mais, le lisseur n’est pas si lisse, car il montre une forme de données très erratique. La moyenne est tirée par deux groupes de données. L’un est représenté par les ventes survenues bien en dessous de la moyenne et les quelques ventes au-dessus. Ce sont des valeurs aberrantes et les personnages essaient de tirer la moyenne à leur avantage. Nous pouvons dire que notre moyenne est en difficulté, parce que les données sont très asymétriques.
Certains avocats plaideraient que les ventes sont plus anciennes et qu’elles doivent être ajustées en fonction du temps. Nous pouvons nous tourner vers les statistiques publiées par les services interagences (SI) sur les prix moyens des maisons vendues à London en 2017, 2018, 2019 et 2020. Avec cette information, nous pouvons déterminer une augmentation annuelle moyenne du prix des maisons qui peut s’appliquer à la superficie en pieds carrés de toutes les ventes. Naturellement, on aurait absolument tort d’utiliser la moyenne d’une base de données d’un SI. La raison en est que, dans quelques années, il pourrait y avoir d’autres maisons vendues dont le prix est plus bas que plus élevé, ce qui affecterait la moyenne pour cette année-là. Le problème se complique d’une année à l’autre, car ces années peuvent voir des ventes de maisons haut de gamme et vice versa. L’asymétrie des séries de données est toujours présente, même si nous avons un plus gros volume de ventes. Au bout du compte, nous ne sommes pas plus avancés d’utiliser des ventes non normalisées pour évaluer ma maison.
D’autres pourraient dire que le problème, c’est que les données ne sont pas ventilées normalement. Qu’est-ce que ça signifie concernant les données de vente et la moyenne ?
Le terme ventilation normale réfère à une série de données qui sont parfaitement reflétées de chaque côté de leur moyenne. Elle a été inventée par Carl Gauss à la fin des années 1800 et on l’appelle également courbe en cloche. Le graphique 2 montre la ventilation normale des données.
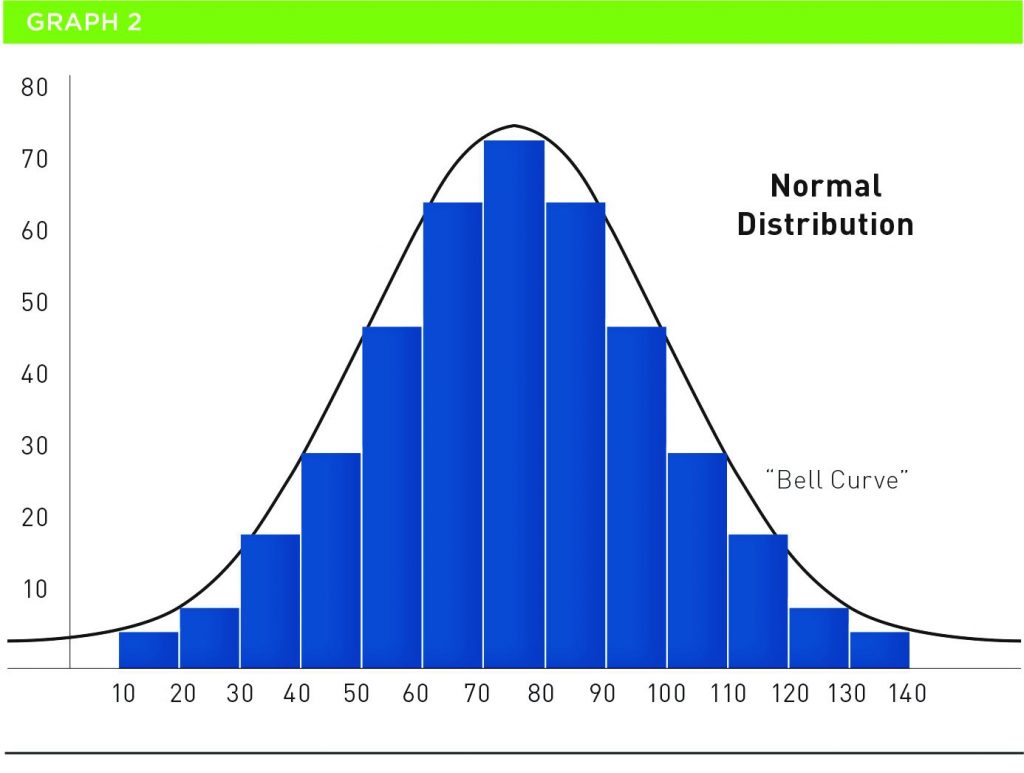
La ventilation normale des données a des propriétés étonnantes. La moyenne, le mode et la médiane des données sont égaux dans la ventilation. Ils peuvent servir efficacement pour l’estimation, alors que les joueurs de cartes français sont connus depuis longtemps pour les utiliser afin d’augmenter leurs chances de gagner. La courbe ne touche pas le bas du graphique parce qu’elle est à l’infini.
Si les données de vente étaient normalement ventilées, l’asymétrie serait éliminée et je pourrais donc utiliser la valeur moyenne de ma maison. Le problème, c’est que les données qui forment la ventilation normale ne sont pas les mêmes que celles de la propriété visée. Les données de vente doivent être ajustées pour les différences résultant du temps, de la grandeur de la maison, de la grandeur du terrain, de la condition, etc. La seule façon de contourner ce problème, c’est de faire en sorte que les ventes formant la ventilation normale soient une réplique exacte de la propriété visée. Il y a bien peu de chances que cela se produise.
À prime abord, l’utilisation de la moyenne des prix de vente des comparables soulève trop de problèmes. La conclusion que l’on pourrait tirer est qu’elle n’a pas sa place dans le processus d’évaluation. Toutefois, ce n’est pas vrai. Par exemple, si nous voulons utiliser la moyenne dans l’unité de comparaison ajustée des ventes des comparables, nous devons comprendre le rôle que jouent deux autres termes statistiques, soit la déviation standard et le coefficient de variation. Nous devons en outre conditionner notre emploi de ces deux outils à une série de ventes ajustée.
Connaître la moyenne de quoi que ce soit n’est pas très instructif, car on ne connaît pas la ventilation ou l’étalement des nombres qui ont produit la moyenne. Si nous disions que le prix moyen d’une maison à London, Ontario, est de 525 000 $, alors que la maison la moins chère s’y est vendue pour 10 000 $ est la plus chère pour 6 500 000 $, alors la moyenne ne veut rien dire. Dans la même veine, si la moyenne était de 525 000 $, alors que le prix de vente le plus bas était de 475 000 $ et le plus élevé de 575 000 $, la moyenne nous en dirait alors plus sur le modèle de ventilation des données. Cela devient plus réaliste.
C’est à Gauss que nous devons la déviation standard. Une citation tirée de la page 460 de l’ouvrage d’Anders Hald, A History of Mathematical Statistics from 1750 to 1930 [Une histoire des statistiques mathématiques, de 1750 à 1930] dit ceci : « Le terme Der mittlere Fehler (ainsi forgé par Gauss – en français L’erreur moyenne) est devenue standard en Allemagne, tandis qu’en Grande-Bretagne, aucune terminologie commune n’a évolué avant que K. Pearson (1894) ne propose le terme ‹ déviation-standard ›, ajoutant entre parenthèses en guise d’explication ‹ erreur du carré moyen ›. Une erreur était remplacée par déviation quand l’application des méthodes statistiques s’étendait aux sciences sociales et biologiques. »
L’un des problèmes avec les termes statistiques comme déviation standard est qu’ils tendent à créer de la confusion. En termes très simples, la déviation standard est « la distance autour de la moyenne qui capture la majorité des ventes dans la série de données ». On peut facilement calculer la déviation standard avec un tableur Excel. Voici un exemple. Le prix de vente moyen des comparables que j’allais utiliser pour évaluer ma maison était de 258,10 $. La déviation standard entourant ce montant est de 72,85 $. Cela signifie que la plupart des ventes tombaient entre 258,10 $ – 72,85 $ = 185,25 $ et 258,10 $ + 72,85 $ = 330,95 $. Tout un étalement. Utiliser la déviation standard sur les données brutes est un bon indicateur que l’évaluateur aura fort à faire pour expliquer et réduire la variation dans la série de données.
L’autre terme employé avec la moyenne est coefficient de variation (CdV). Coefficient signifie que le nombre et la variation sont simplement la différence ou l’étalement. Nous pouvons calculer le CdV en prenant la déviation standard x 100 % et en la divisant par la moyenne. Dans notre cas, le pourcentage du coefficient de variation (CdV %) est de 28,22 %. Le CdV % cristallise la moyenne et la déviation standard dans un nombre particulier. Des plus critiques, ce nombre peut être utilisé comme point d’appui pour l’évaluation dans la MCD.
Dans l’analyse des points de qualité (PQ), toute la MCD se focalise sur le CdV. Voici un exemple tiré de l’évaluation récente d’un bureau converti. Le graphique 3 montre le prix de vente ajusté par pied carré de bâtiment par point.
Dans le tableur des PQ, la moyenne, la déviation standard et le CdV sont calculés automatiquement, montrant que le CdV % est descendu à 4 %. Comme l’étendue non normalisée des prix de vente pour les ventes ‹ entrant › dans l’analyse était de 55 %, notre modèle d’évaluation avec un CdV % de 4 % paraît bien alors.
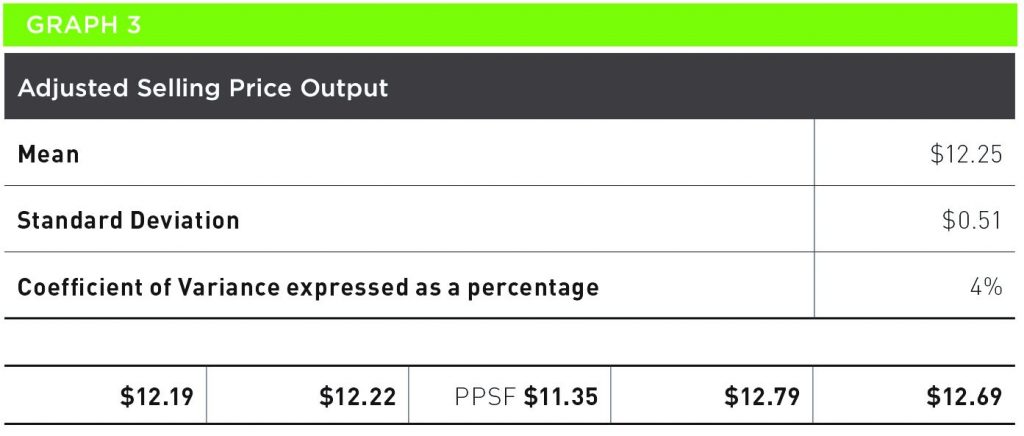
Le graphique 4 démontre en outre comment la valeur marchande de la propriété visée était calculée en employant la moyenne et la déviation standard.
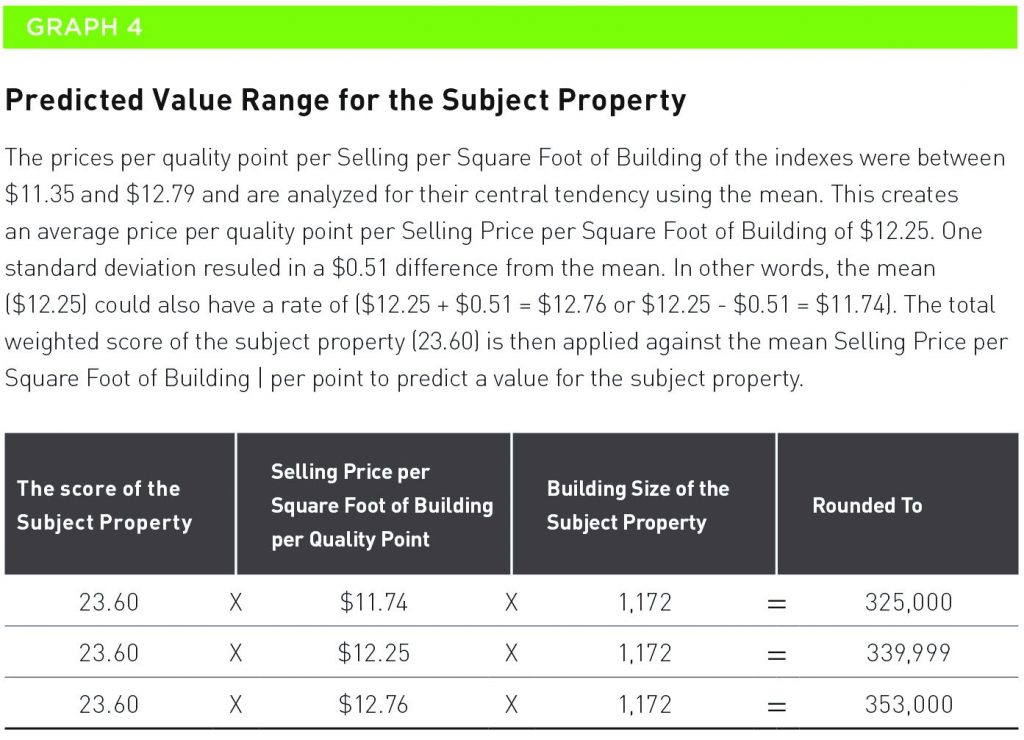
La déviation standard est le nombre qui créé l’étendue autour de la moyenne après les ajustements. C’est logique, puisqu’il doit y avoir une certaine étendue dans les valeurs potentielles de la propriété, étant donné que les acheteurs éventuels n’offriront pas tous le même prix.
Il est à noter que la déviation standard autour de la moyenne n’a rien à voir avec les probabilités. Elle capture simplement la distance autour de la moyenne où tombe la majorité des prix de vente des comparables (après ajustements). Plus le CdV est bas autour de cette moyenne, mieux c’est, parce que ça signifie que l’étendue des prix de vente ajustés est plus serrée.
Le CdV comme test de fiabilité pour utiliser le prix de vente ajusté moyen des comparables est un nombre critique. Par exemple :
Le prix de vente ajusté par pied carré de bâtiments commerciaux est de 100,00 $ – 120,00 $ – 135,00 $ – 150,00 $.
La moyenne est de 126,25 $ et la déviation standard est de 18,49 $. En utilisant le CdV %, ça donne 14,64 %. Nous conseillerions à l’évaluateur de retourner à la planche à dessin pour voir s’il peut réduire encore plus la variation des prix de vente ajustés.
Mais, que se passe-t-il si le prix de vente ajusté par pied carré de bâtiments commerciaux est de 120,00 $ – 125,00 $ – 124,00 $ – 122,00 $ – 126,00 $ ? La moyenne est de 123,40 $ avec un CdV % de 2,15 %.
Maintenant, cet évaluateur dispose d’un modèle d’évaluation plus fiable et peut employer la moyenne de 123,40 $ comme une façon d’évaluer, plus et moins le 2,15 %. La valeur de la propriété tomberait quelque part dans cette fourchette.
Nous ne devrions pas limiter l’usage de la moyenne à la MCD. Elle peut aussi s’appliquer aux taux de capitalisation globaux et au multiplicateur de revenu brut (MRB). Cependant, ce dernier doit être utilisé pour rendre égaux les attributs la propriété visée et ceux des ventes.
Conclusion
Utiliser les prix de vente non ajustés des ventes comparables, peu importe leur perfection apparente, est une mauvaise façon d’évaluer l’immobilier. On doit toujours tenir compte des différences entre les ventes et la propriété visée. Aussi, la majorité des variations entre les ventes n’est pas toujours visible en surface et c’est pourquoi un ordinateur est nécessaire au processus d’ajustement.
Nous pouvons utiliser la moyenne comme un nombre fiable, à ces trois conditions :
- L’unité de mesure moyenne est après les ajustements.
- Le CdV % doit être un faible nombre, disons en dessous de 5 %.
- L’étendue des valeurs de la propriété sera +/- le CdV % autour de la médiane ou de la moyenne.
Des commentaires reçus d’autres évaluateurs sont à l’effet que le CdV % ne peut être inférieur à 10 %. Est-ce qu’il existe un certain nombre standard autour de la moyenne qui pourrait être un indicateur de ventes bien ajustées ? La réponse est non. Si l’on ne peut obtenir un CdV % de moins de 5 %, cela pourrait signifier qu’on utilise les mauvais comparables, que les ajustements sont incorrects ou, peut-être, vu la rareté de la propriété évaluée, qu’un CdV % autour de 10 % est acceptable.





