Application de l’analyse de régression multivariée aux questions d’expropriation
Évaluation immobilière au Canada
Rechercher dans la bibliothèque en ligne
Par George Canning, AACI, Canning Consultants Inc., London, Ontario
L’effet préjudiciable peut être la forme d’indemnisation foncière la plus difficile à prouver devant une cour de justice. La réclamation d’une indemnisation est un droit prévu par la loi, mais ne signifie pas l’admissibilité. Souvent, l’indemnisation n’est pas quantifiable en raison des données insuffisantes, des complexités de leur analyse et de la méconnaissance des méthodes avancées requises pour faire « parler » les données. Dans ces cas, le droit à une indemnisation peut aboutir à la conclusion « difficile à prouver » ou « pas assez de données » et, subséquemment, être classé dans le cosmos « encore à figurer » de l’analyse de données exploratoires fragmentées.
Le présent article traite de la principale utilisation d’une analyse de régression multivariée en ce qui concerne les questions d’indemnisation foncière, en plus de présenter brièvement une autre forme d’analyse de données quand celles-ci tendent à être « minces ». J’ai rédigé cet article pour aider les professionnels de l’évaluation qui veulent utiliser des méthodes d’analyse de données plus sophistiquées afin de résoudre les réclamations pour effet préjudiciable. Je ne prétends pas que l’emploi de ces outils garantira au demandeur le droit à une indemnisation, mais ils brosseront pour l’expert immobilier un portrait plus détaillé des données lorsque la méthode de comparaison directe ne produit pas de conclusions utiles.
Les réclamations d’indemnisation foncière pour des questions d’effet préjudiciable telles que perte de stationnement, réduction de la marge de recul d’une cour avant, augmentation du débit de circulation, perte de vue, droits d’exploitation souterraine et application cohérente de la méthode traditionnelle « avant » et « après », sont des problèmes immobiliers pouvant être résolus grâce à l’analyse de régression multiple.
Problèmes posés par l’analyse de données
Les données se trouvent sur le marché et elles tendent à se comporter de façon irrégulière. Ce que vous croyez que les données tentent de dire et ce qui survient en réalité sont souvent deux choses distinctes. Sans une analyse appropriée des données immobilières, la réponse à une réclamation pour effet préjudiciable peut être ensevelie sous une pile d’attributs de propriété bruts. Afin de « disperser le brouillard », la réalisation d’une analyse de régression multiple peut fournir au professionnel de l’évaluation les motifs prépondérants de la réclamation et le montant approprié du règlement. Inversement, l’admissibilité de la réclamation pour « dommage » peut être absente, mais apparaîtra au grand jour en testant les données de vente de façon plus « robuste ».
Le problème avec les données immobilières découle du fait qu’elles ne sont pas structurées et s’expriment à la fois sous forme numérique et non numérique. Toutefois, la fonction sous-jacente d’une analyse de données immobilières est de réduire l’incertitude. Une plus grande certitude sur le comportement des données immobilières permet de prendre de meilleures décisions sur leur valeur et améliore l’incidence particulière d’une variable de propriété sur l’explication d’un dommage pour effet préjudiciable.
L’analyse de régression n’est pas parfaite, mais elle possède d’excellents attributs qui en font une option souhaitable pour prouver le bien-fondé des réclamations pour effet préjudiciable ou pour les rejeter.
Premièrement, elle aide à organiser les données et permet d’explorer la forme la plus élémentaire d’une analyse de données : le graphique. L’image suivante est un bon exemple d’emploi de graphiques pour aider à décrire des données. Mais il faut faire attention, car les présentations visuelles peuvent être trompeuses.
Tracé en boîte du prix de vente par superficie affectée
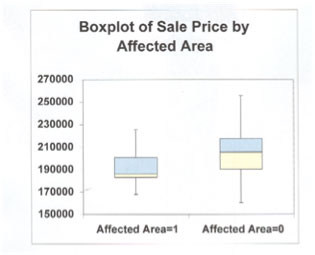
Les lignes rouges du tracé en rectangle ci-dessus représentent le prix de vente moyen pour deux jeux de données. Le premier représente les terrains affectés par un contaminant et le second les terrains non affectés. On constate que les terrains affectés se sont vendus pour environ 187 000 $, alors que les terrains non affectés se sont vendus pour 205 000 $. Après avoir appliqué tous les attributs de propriété au jeu de données, on a conclu qu’il n’y avait pas beaucoup de différence entre les prix. Voici quelques mises en garde. L’analyse de données numériques devrait aller de pair avec leur présentation visuelle. On pourrait défendre l’opposé de cette affirmation. Le recours au prix moyen d’un groupe de données sans un graphique est risqué. Voir la forme des données pourrait donner à penser que la moyenne n’est pas représentative et qu’une expression plus adéquate serait la médiane ou le mode. C’est pourquoi aucun évaluateur ne devrait se fier au « prix annuel moyen des maisons vendues » d’un système inter-agences (i.e. MLS), par exemple. Le prix moyen donné n’est qu’un nombre.
Ce nombre devient plus pertinent quand on connaît les limites du prix moyen et des attributs causant ces différences. C’est comme si l’on disait « tous les terrains sont pareils parce qu’ils ne sont que de la terre ».
Deuxièmement, l’analyse de régression peut servir à explorer le rapport qui existe entre les variables. En tant qu’évaluateurs, nous pensons parfois que seulement certaines variables spécifiques influencent le prix des propriétés immobilières. Une simple exploration de vos données à l’aide d’un programme de régression vous permettra peut-être de constater que le contraire est aussi vrai. Le revenu n’est pas toujours le seul élément moteur des « propriétés à revenus », par exemple. Parfois, les attributs des données interagissent et produisent l’affichage des caractéristiques de propriété n’ayant possiblement jamais été mises en images. Cependant, des attributs de propriété similaires peuvent fausser le portrait des données, car l’une essaie de dominer l’autre.
Troisièmement, le trait le plus frappant d’une analyse de régression multiple est sa capacité d’assurer la stabilité de toutes les variables en explorant chacune d’elles de manière indépendante.
Même si la formule de l’analyse de régression peut s’exprimer de plusieurs façons différentes, sa fonction de base n’a pas changé depuis son invention par Sir Francis Galton en 1820.
Y = AX + B
Il est possible de modifier l’équation ci-dessus en lui ajoutant d’innombrables variables, comme dans l’exemple ci-dessous.
Y=a+b1*X1 +b2*X2 +…
L’élément b1*X1 pourrait représenter les dimensions de la maison, alors que b2*X2 pourrait représenter son âge. Ça pourrait aller à l’infini et le nombre de variables utilisées dans l’équation est directement lié à la quantité de données. C’est ce qui fait de l’analyse de régression un outil de données si puissant. Le modèle attribue un coefficient ou un nombre à chaque variable, faisant en sorte que tous les autres demeurent stables. Cela équivaudrait à geler la vente de cinq maisons, alors que l’évaluateur les visitant verrait une plaque montrant la valeur de chaque attribut de la propriété.
Ci-dessous apparaît le cas traitant de la « prise en possession » pour l’élargissement d’une voie de circulation. Cette expropriation soulevait deux possibilités d’effet préjudiciable ou deux réclamations potentielles : 1) perte de valeur due à une réduction de la marge de recul de la cour avant; et 2) perte de valeur due à une augmentation du débit de circulation. Les graphiques suivants dénotent un modèle distinctif de ces réclamations.
Circulation

Marge de recul
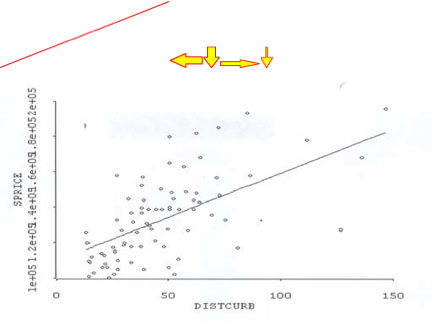
Le graphique de gauche montre la ligne de régression à pente négative, alors qu’augmentent les recensements de la circulation de gauche à droite. Même si les recensements de la circulation sont en hausse, le prix de vente sur l’axe « Y » diminue. Le graphique de droite montre la ligne de régression à pente positive, alors les marges de recul diminuent le long de l’axe « X » de gauche à droite. Le prix de vente correspondant sur l’axe « Y » montre une baisse de valeur quand les marges de recul décroissent. Mais comment les données réelles produites équivalent-elles à ce que les graphiques évoquent ?
Résultats de l’exécution de régression
L’analyse de régression ne consiste pas à tracer une ligne rouge à travers deux jeux de données. Les deux graphiques ci-dessus illustrent le rapport entre deux variables (marges de recul et débit de circulation) par rapport au prix de vente. Ce serait une erreur de tracer une ligne vers le haut à partir des recensements de la circulation jusqu’au prix de vente pour une indication de perte. C’est une méthode d’analyse imprécise, car les graphiques ci-dessus nous disent seulement qu’il y a un rapport tangible entre ces deux variables et le prix de vente. Ce n’est peut-être rien de plus qu’un faux rapport entre les marges de recul et le débit de circulation par rapport au prix de vente. Par contre, il existe un certain nombre d’autres caractéristiques de propriété qui doivent entrer dans l’analyse de régression et faire partie de l’« exécution de régression » et qui peuvent également expliquer ces rapports.
Ce qui suit était une « exécution de régression » de la base de données, qui consistait en 81 observations représentant des propriétés similaires (non identiques) à la propriété sujet.
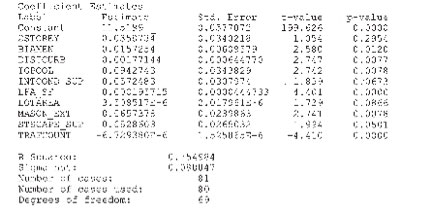
Recensements de la circulation
L’incidence des recensements de la circulation sur les données est illustrée par le coefficient -6,729380E-6. La statistique « T » apparaît comme -4,410. Ces deux nombres sont négatifs parce que l’augmentation du débit de circulation a un impact négatif sur le prix vente.
La statistique « T » est seulement une mesure de l’importance. En d’autres mots, l’évaluateur est-il assez confiant que les résultats du coefficient -6,729380E-6 sont statistiquement significatifs et ne sont pas simplement apparus de manière aléatoire ? En règle générale, un score « T » de plus de deux indiquerait que le résultat obtenu n’est pas dû au hasard. On peut le vérifier avec la valeur p – 0,000. Les valeurs p sont des probabilités et sont généralement établies pour un niveau de 5 %. Un nombre supérieur à 5 % signifierait que le coefficient obtenu avec le modèle de régression serait le plus vraisemblablement apparu par hasard. Ainsi, une valeur p inférieure à 5 % indiquerait que le coefficient résultait d’un facteur autre que le hasard. La valeur p de 0,000 pour le coefficient du recensement de la circulation est de moins de 5,0 %.
L’élément -6,729380E-6 est en notation scientifique et signifie en réalité que, pour chaque changement dans un recensement de la circulation, le prix de vente diminuait de ,000006729380 dollars. Si nous prenons 10 000 voitures comme base de référence, ce nombre changerait à 0,06729. Si nous voulions convertir ce dernier nombre en pourcentage, il faudrait le multiplier par 100 % comme suit : 0,06729 x 100 % = 6,729 % (arrondi à 6,73 %). Cela veut dire que, pour chaque changement dans les recensements de la circulation de 10 000 voitures, le prix de vente chutait de 6,73 %. Dans le cas de la propriété sujet, les recensements de la circulation effectués avant la « prise en possession » sont de 23 000 voitures par jour, qui augmenteront avec le temps à 33 000 voitures, ce qui représente une différence de 10 000 voitures.
Par conséquent, la valeur de la propriété sujet subirait un impact négatif de 6,73 %. Il faut considérer deux choses dans l’application de ce pourcentage à la propriété sujet. La première est que la hausse des débits de circulation ne se produira pas immédiatement. Cela voudrait dire qu’à la date effective de l’évaluation, le 6,73 % serait escompté, car le recensement de la circulation plus élevé surviendrait seulement dans le futur. L’évaluateur a décidé d’appliquer le plein effet des recensements de la circulation à la propriété sujet, car ces futurs recensements de la circulation ne sont que des estimations. La deuxième chose à considérer est que l’impact d’une augmentation des recensements de la circulation, ainsi que les autres variables déterminantes, s’appliquerait à la propriété sujet en fonction de sa valeur « résiduelle » (une fois la valeur du terrain « pris en possession » et les dommages-intérêts imputables à des troubles de jouissance soustraits de la valeur de la propriété sujet « avant » la « prise en possession »).
Marge de recul
La marge de recul variable indiquait un coefficient de 0,00177144. La statistique « T » apparaît comme 2,747. La valeur p est de 0,0077. Le coefficient de 0,00177144 peut s’exprimer par un pourcentage en multipliant par 100 %. Donc, l’incidence des marges de recul sur le prix de vente est de 0,00177144 x 100 % = ,177144 %. Cela signifie que, pour chaque pied de diminution de la marge de recul, le prix de vente était touché par ce montant. La marge de recul de la propriété sujet aura perdu 33 pieds « après » la « prise en possession ». L’impact du pourcentage est de 33 pieds x ,177144 % = 5,85 %.
L’analyse de régression a conclu qu’il existe sur le marché des évidences que la propriété sujet subira un quelconque « effet préjudiciable » suite à la « prise en possession ». Le doute est critique dans les cas d’expropriation. Le Land Compensation Board est très clair sur le « doute ». Le livre New Law of Expropriation, à la page 10-150, paragraphe 1,7, stipule :
« S’il existe un doute quant au moment où un demandeur est devenu conscient d’un effet préjudiciable, ce doute doit être résolu en faveur de celui-ci. Lorsqu’un témoin contre-interrogé a admis qu’il croyait que certains dommages s’étaient accumulés depuis le premier, le Conseil a observé que rien n’indiquait ce qu’entendait le témoin en employant le terme « depuis le premier ». En l’absence de preuves probantes quant au moment où les dommages sont survenus ou sont devenus connus du demandeur, la réclamation pour effet préjudiciable peut être reçue. »
Dans le cas ci-dessus, l’affaire s’est réglée et une indemnisation a été versée au propriétaire foncier, sans aller en arbitrage ou faire appel au tribunal administratif.
À quoi ressemble un graphique de régression multivariée ?
Si on regardait l’affichage graphique d’une analyse de régression multiple, ça ressemblerait à ce qui suit :
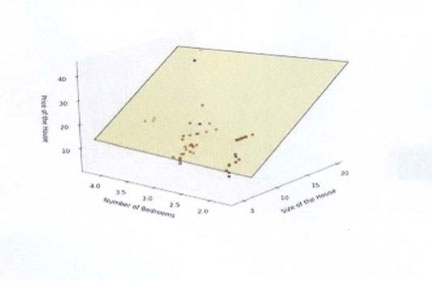
La série de points ci-dessus représente le nombre de pièces et les dimensions des maisons mis en relation avec le prix de vente. La boîte jaune/verdâtre est la ligne de régression, qui est tridimensionnelle car nous avons ici plusieurs variables. En fait, la technologie pour afficher une ligne de régression comportant beaucoup plus de variables n’a pas encore été inventée au moment d’écrire ces lignes.
Un des problèmes avec l’analyse de régression est qu’elle est avide de données. Comme plusieurs variables ou caractéristiques de propriété peuvent causer ou expliquer les différentiels de prix, on doit disposer d’une quantité de données correspondant à chacune d’elles. Si vous avez trop de variables et pas assez de données de vente, vous rencontrerez un problème de « degrés de liberté ». Une phrase savante pour dire que, fondamentalement, on en demande trop aux données.
Le résultat est que la régression attribuera une pénalité. En règle générale, chaque variable sélectionnée devrait reposer sur 7 à 10 ventes.
La plupart des évaluateurs se diraient assez chanceux de trouver 5 à 10 ventes pouvant apporter des évidences pour une réclamation pour effet préjudiciable ou en confirmer son absence. Dans ces cas, la méthode qualitative et quantitative appelée « point de qualité » pourrait être l’outil à employer. Le meilleur exemple se trouve dans le traité Property Valuation and Analysis, 2e édition, de RTM Whipple, publié par Lawbook Co., 2006, ISBN #0 455 22394 7. Plus près de nous est le livre Readings in Canadian Real Estate, 4e édition, de Gavin Arbuckle et Henry Bartel, Captus University Publications, BSN #1-55322-062-5. J’ai écrit il y a longtemps un article intitulé The Contemporary Direct Comparison Approach to Value, traitant des petites bases de données utilisant le « point de qualité ».
Apprendre davantage sur ces outils avancés
Avant de vous précipiter pour acheter tous les livres possibles sur l’analyse de régression, je vous conseille d’y aller une étape à la fois et de commencer par des livres sur la statistique de base et l’analyse de données élémentaires. Ceci pour deux raisons :
- La statistique possède son propre langage et vous devez le comprendre.
- L’analyse de données exploratoires peut décourager tout bon évaluateur très vite. Elle est un voyage à la découverte de soi, pas seulement sur notre perception des données, mais aussi sur sa méthode de présentation et, surtout, sur ce que les données nous disent.
Pour en savoir plus sur l’analyse de régression, veuillez consulter le menu latéral des publications sur l’analyse de régression dans l’édition électronique interactive de la revue Évaluation immobilière au Canada (www.aicanada.ca).
Conclusions
Les marchés immobiliers sophistiqués ainsi que les réclamations pour dommage en vertu de la Loi sur l’expropriation nécessitent de bons outils diagnostiques pour séparer le « blé » de l’ « ivraie ». La modélisation de la régression a sa place pour décrypter les problèmes immobiliers complexes. Je dois à la vérité de dire que l’analyse de régression ne s’applique pas facilement à tous les cas d’effet préjudiciable. Analyser les résultats peut être difficile, en particulier dans les cas où les preuves sont ténues pour une réclamation. Ça peut être compliqué, mais l’univers des données immobilières l’est aussi. Les données ne révèlent pas leurs secrets facilement et même en « exécutant » quelques régressions, elles montreront possiblement que la réclamation pour effet préjudiciable peut être apparente, faible ou inexistante. Au moins avec l’analyse de régression, l’expert immobilier est plus près de découvrir la vérité grâce à de bonnes compétences d’analyse.
On a souvent dit que l’explication la plus « simple » de dommages résultant d’un effet préjudiciable est la mieux présentée pour que les arbitres, juges et présidents puissent la comprendre. De mon point de vue, cet énoncé n’a aucune valeur, car nous vivons à une époque où de gros blocs de données sont déjà disponibles sur l’Internet. Mes conversations avec des évaluateurs américains qui traitent des condamnations (réclamations d’indemnisation foncière) indiquent que les avocats retournent sur les bancs d’école pour mieux comprendre l’emploi d’une analyse de données, notamment l’analyse de régression. Des lectures intéressantes comprennent Statistical Evidence in Litigation de Will Yancey, PhD; Multiple Regression in Legal Proceedings, 80 Columbia Law Review 702, de Franklin M. Fisher; ou Statistics for Lawyers and Law for Statisticians, 89 Michigan Law Review, de David H. Kaye.
Je crois que rien n’est plus facile à utiliser que des graphiques pour expliquer ou défendre une réclamation pour effet préjudiciable. Mais les mathématiques sont nécessaires pour appuyer le montant indemnisable.
Qu’on aime les statistiques ou non, elles sont utilisées plus que jamais dans le monde de l’analyse immobilière. Par exemple, aux cours que j’ai suivis récemment sur l’analyse de données avec COURSEA, 55 000 personnes s’étaient inscrites à des cours élémentaires sur le sujet.
L’analyse de données permet au professionnel de voir des modèles de données immobilières, qui étaient impensables il y a 10 ans. Elles donnent des aperçus sur la composition des données et sur la manière dont les variables de propriété aident à expliquer la variation des prix de vente. Après tout, n’est-ce pas là le travail du professionnel de l’évaluation ?
Pour en savoir plus sur l’analyse de régression
Si vous aimeriez en apprendre davantage sur l’analyse de régression, vous pouvez commencer par lire les livres primés suivants, écrits par Dawn Griffiths et publiés par O’Reilly :
- Head First Statistics
- Head First Data Analysis
Ils peuvent être en format PDF, alors essayez sur www.headfirstlabs.com.
Ce matériel est excellent, car il traite les lecteurs comme s’ils ne connaissaient rien aux statistiques. Il contient beaucoup de croquis à main levée et d’images. Ces livres abordent l’analyse de régression en toute simplicité. Ils sont plus conçus pour vous faire réfléchir à l’analyse de données qu’aux outils particuliers qui servent à effectuer celle-ci.
Votre conseil scolaire local est une autre source riche en livres sur les statistiques et sur l’analyse de régression. Enseigné aux années supérieures, le sujet constitue un très bon point de départ.
On écrit souvent les livres sur l’analyse de régression à un très haut niveau, mais les livres suivants peuvent être utiles :
1. Multiple Regression: A primer, Paul D. Allison, Pine Forge Press. USBN # 0-7619-8533-6.
2. Applied Regression Analysis, Linear Models, and Related Methods, John Fox, Sage Publications. USBN # 0-8039-4540-x.
3. Correlation and Regression Analysis, A Historian’s Guide, Thomas J.
Archdeacon, The University of Wisconsin Press. USBN # 0-299-13650-7.
Une autre bonne ressource est COURSERA, un programme mis en ligne par différentes universités à l’échelle du monde sur une variété de sujets, incluant les statistiques. L’avantage avec COURSERA, c’est qu’il est gratuit. Mais n’allez pas croire que ce sera de tout repos. Il y a souvent 6 à 10 heures de devoirs à faire chaque semaine, surtout si vous souhaitez obtenir un crédit auprès de l’ICE.
Sans aucun doute, il faut absolument faire la lecture de Quantitative Techniques in Real Estate Counseling, de Gene Dilmore, d’autant plus qu’il traite de l’analyse de régression dans plusieurs chapitres. Publié par Lexington Books (ISBN #0-669-98251-2), c’est un bon vieux livre qui vous sera précieux. C’est Gene Dilmore qui a inventé le terme « point de qualité » et qui a aidé le Dr Graaskamp à élaborer le modèle que nous connaissons aujourd’hui.
-30-





